コレクション ピタゴラス��定理 計算方法 247454-ピタ��ラスの定理 計算方法
2次元ベクトルの大きさを求める式 2次元ベクトル (x,y)の場合は、ピタゴラスの定理で簡単に大きさを求めることができます。 2次元ベクトル (x,y)の大きさ = √ x² y² 例 2次元ベクトル (1,80)の大きさ (長さ)を求める = √ 1² 80² = √ 6400 = √ 800
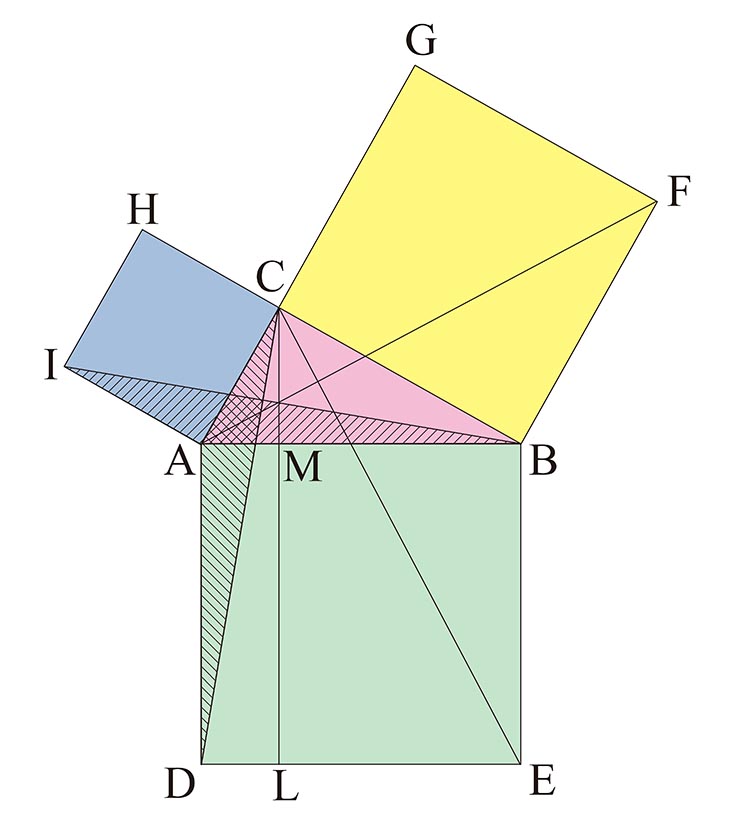
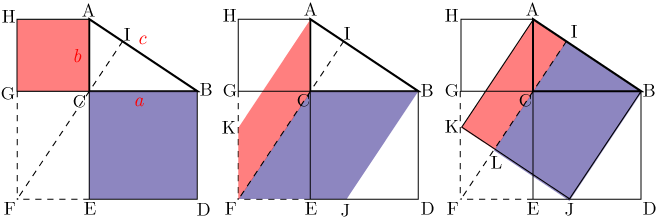
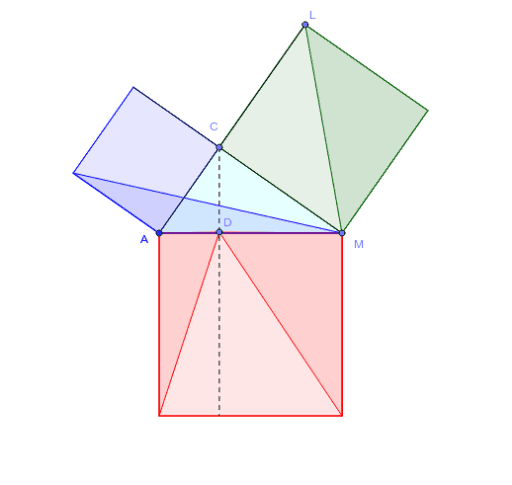
ピタゴラスの定理 計算方法- 三平方の定理の証明は、紀元前からあらゆる人があらゆる方法で考え出してきました。 この記事では、「モナ・リザ」や「最後の晩餐」で有名な 芸術家レオナルド・ダ・ヴィンチが考案した証明方法 を、 現役数学教員がわかりやすく解説 します。 ユークリッドと同様の図に補助線を加えピタゴラスの定理、小学生バージョン 2つの長方形ABCDとEBFCが図のように重なっています。 長方形EBFCの面積は何cm2になりますか。 ↓こちらファミリーページにもどうぞ! どう解く? 中学受験算数 算数オリンピック問題に挑戦! これが中学入試に出た
ピタゴラスの定理 計算方法のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
 |  |  |
「ピタゴラスの定理 計算方法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「ピタゴラスの定理 計算方法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 | ||
「ピタゴラスの定理 計算方法」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  |  |
 |  | |
「ピタゴラスの定理 計算方法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 | ||
「ピタゴラスの定理 計算方法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | 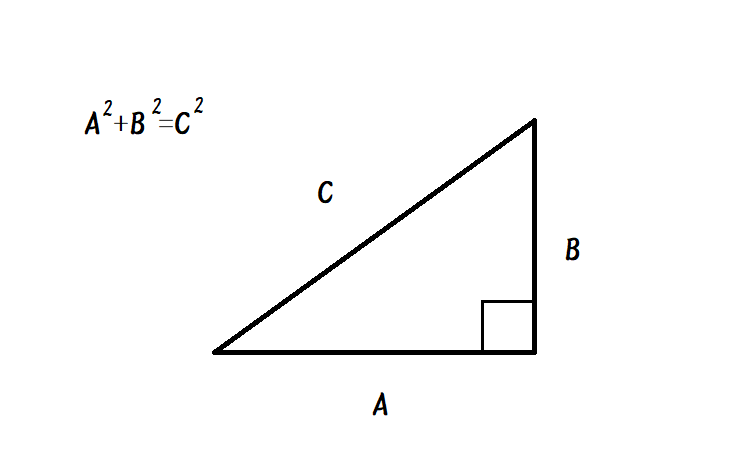 |
 |  | |
 |  |  |
「ピタゴラスの定理 計算方法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「ピタゴラスの定理 計算方法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「ピタゴラスの定理 計算方法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |
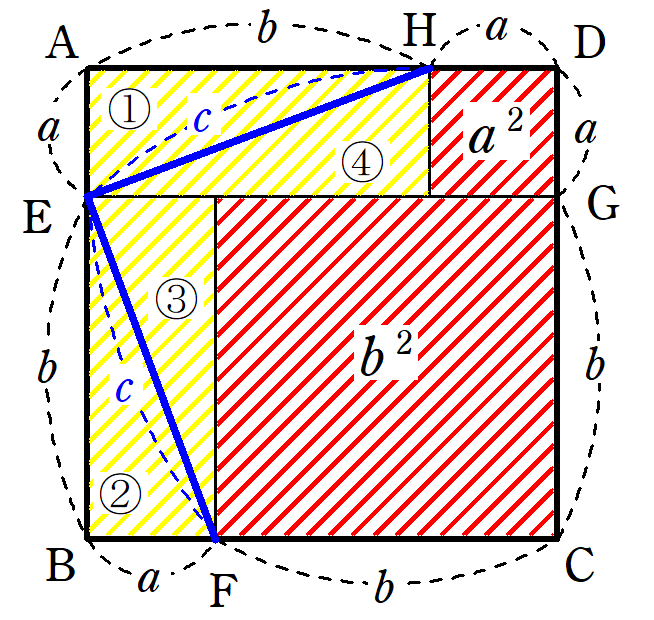
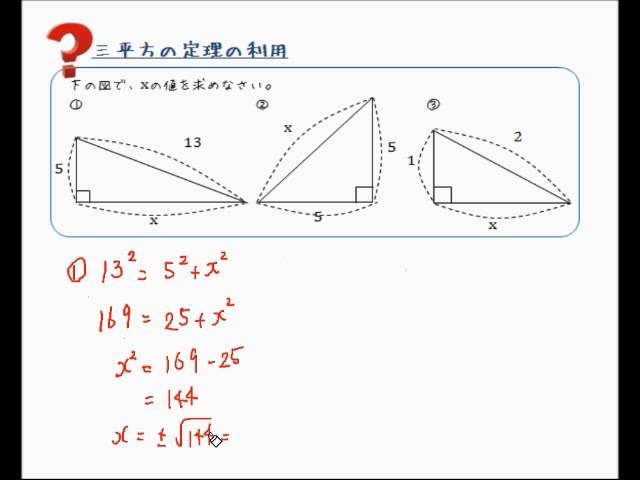
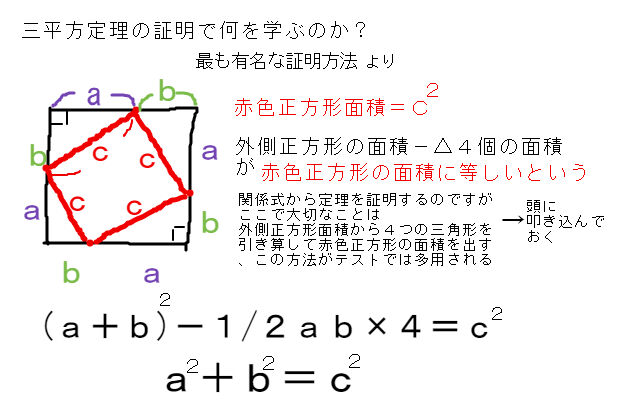
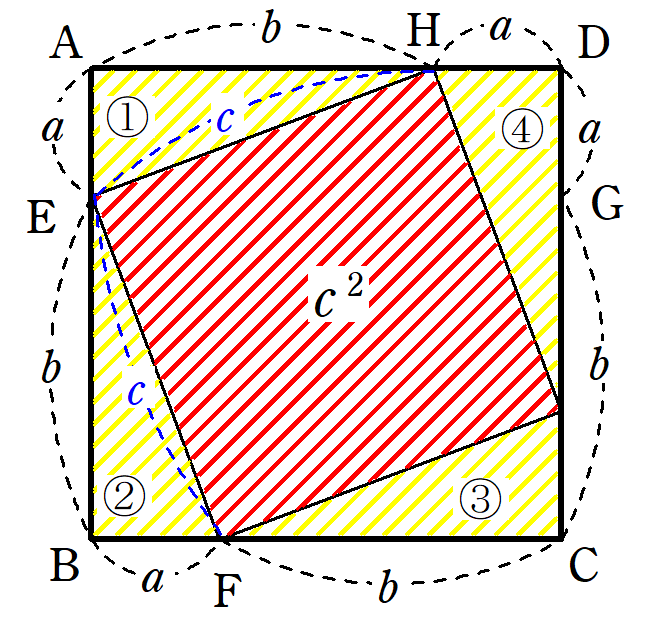
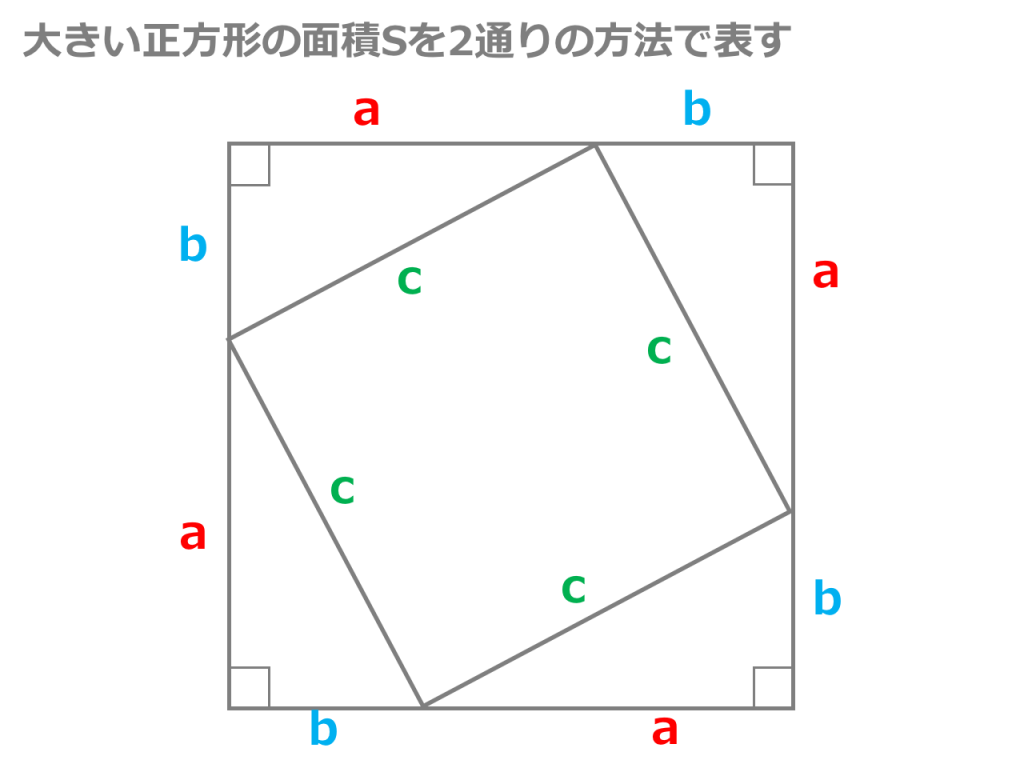
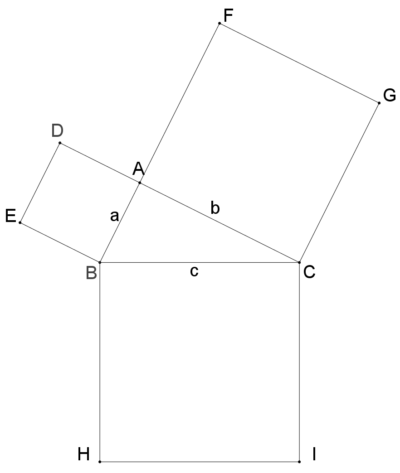
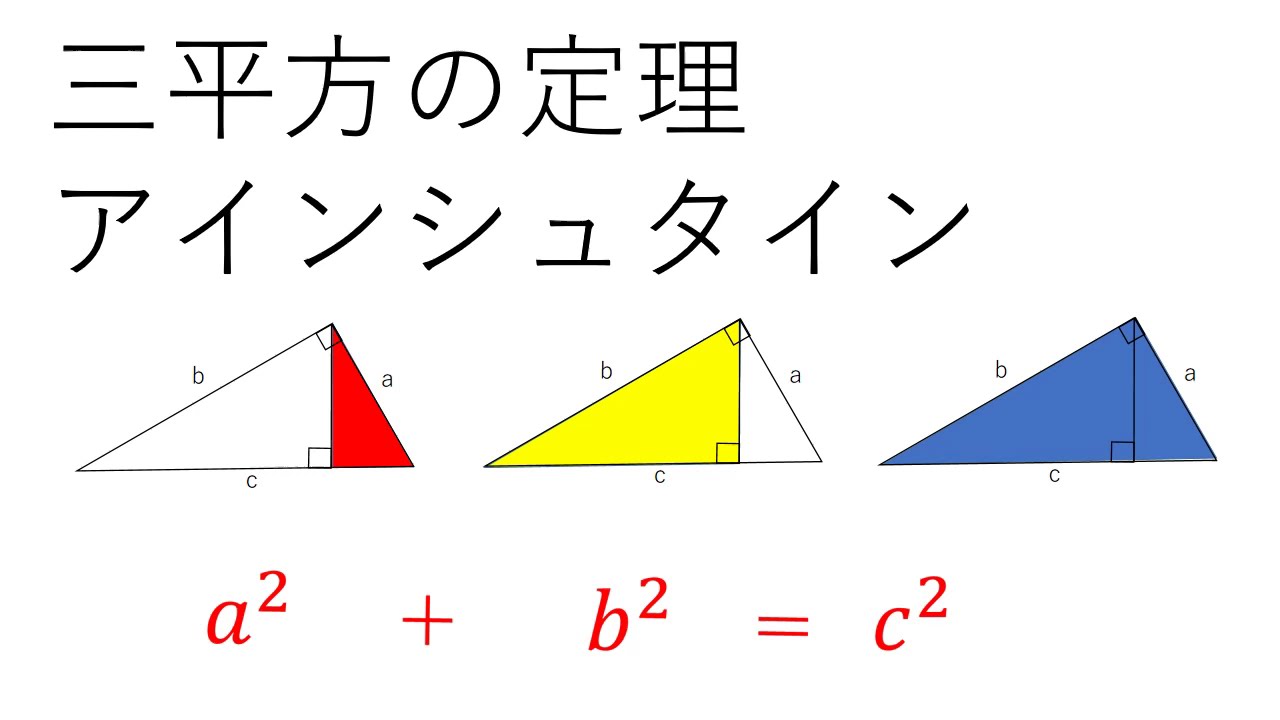
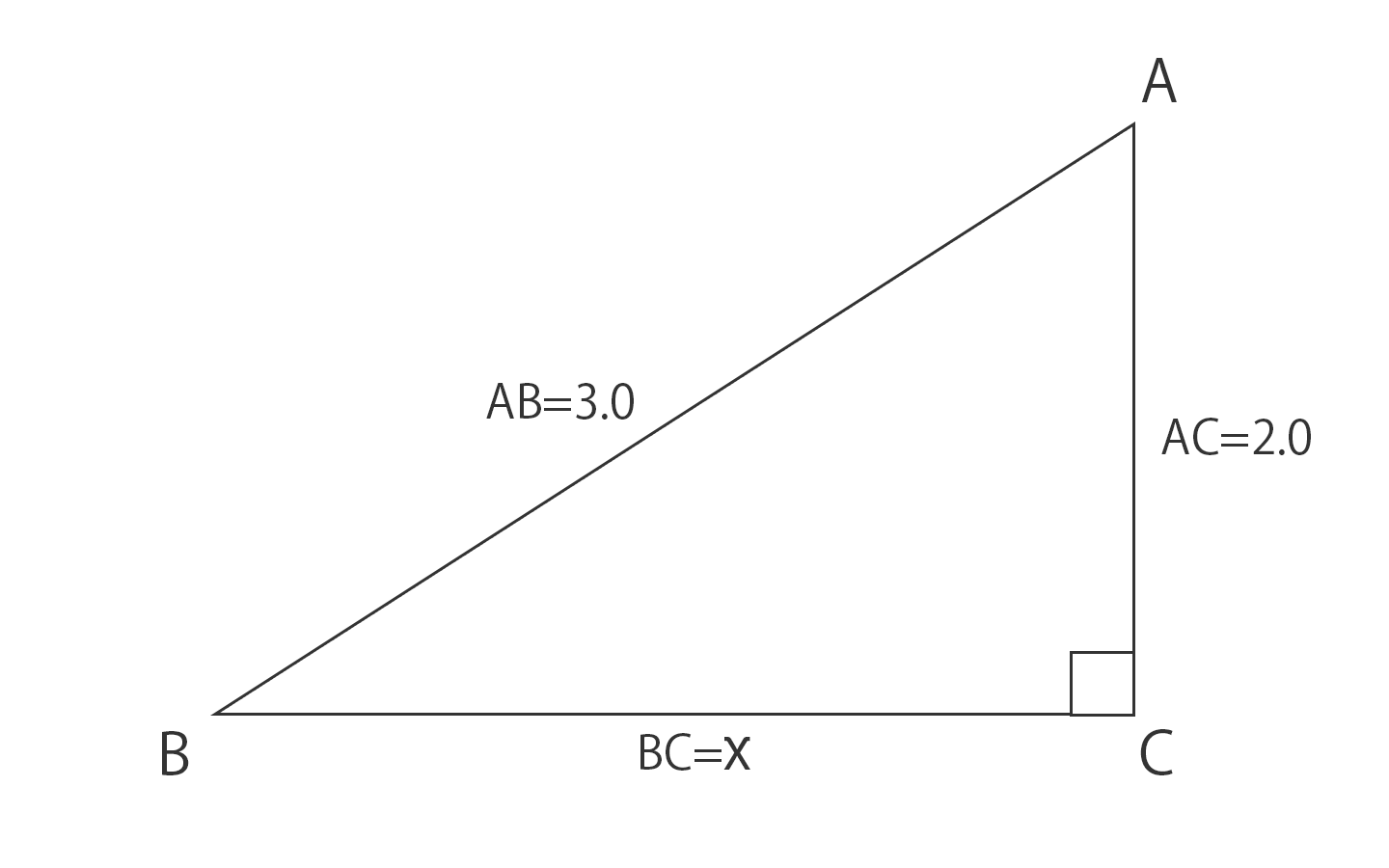
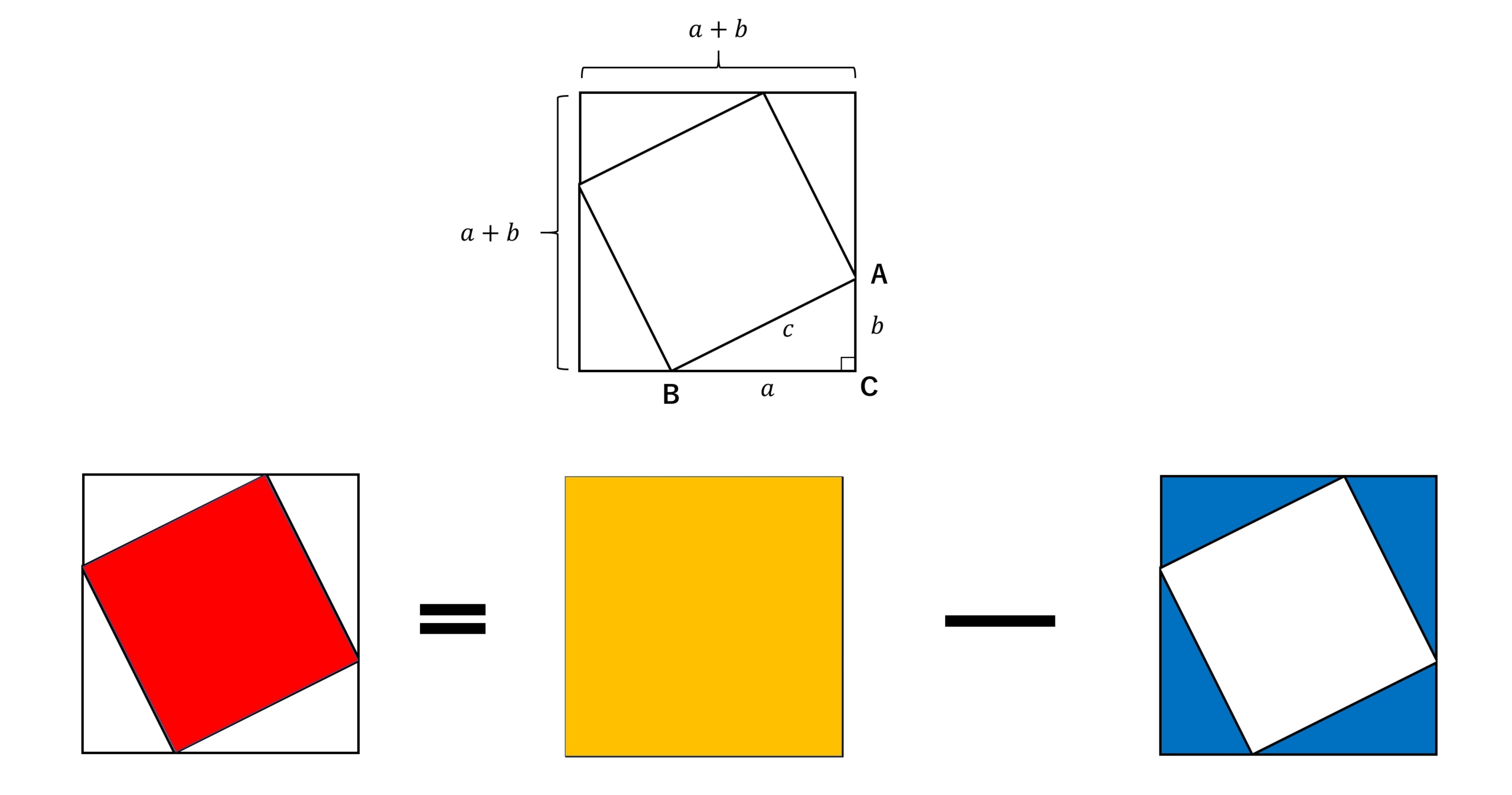
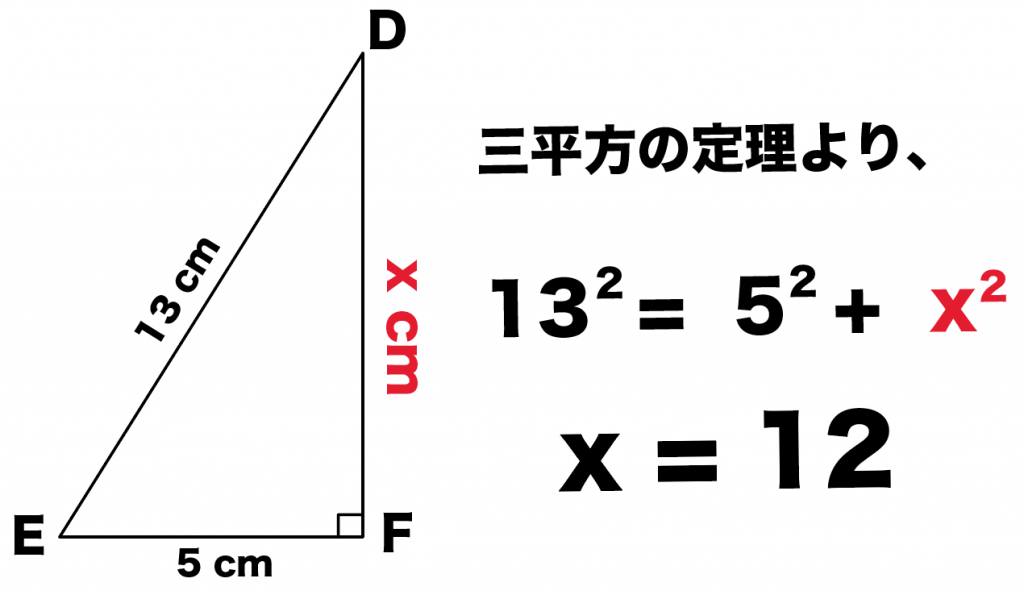
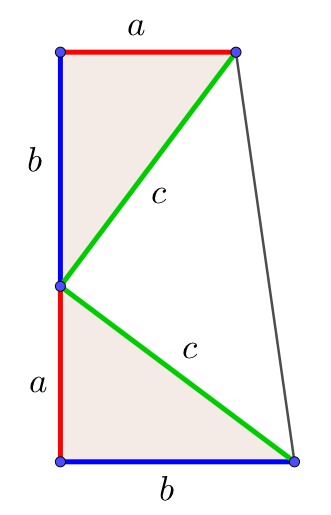
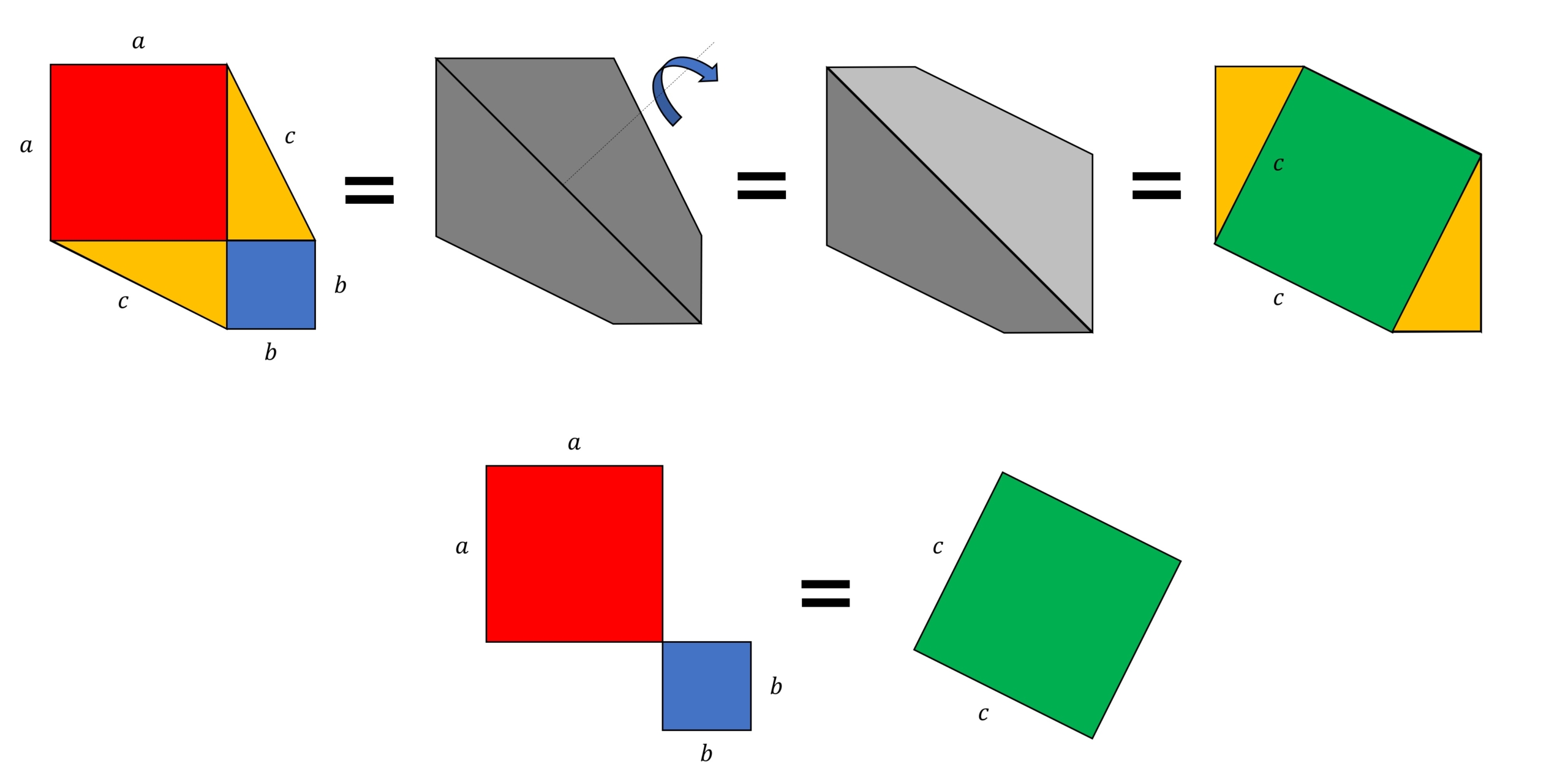
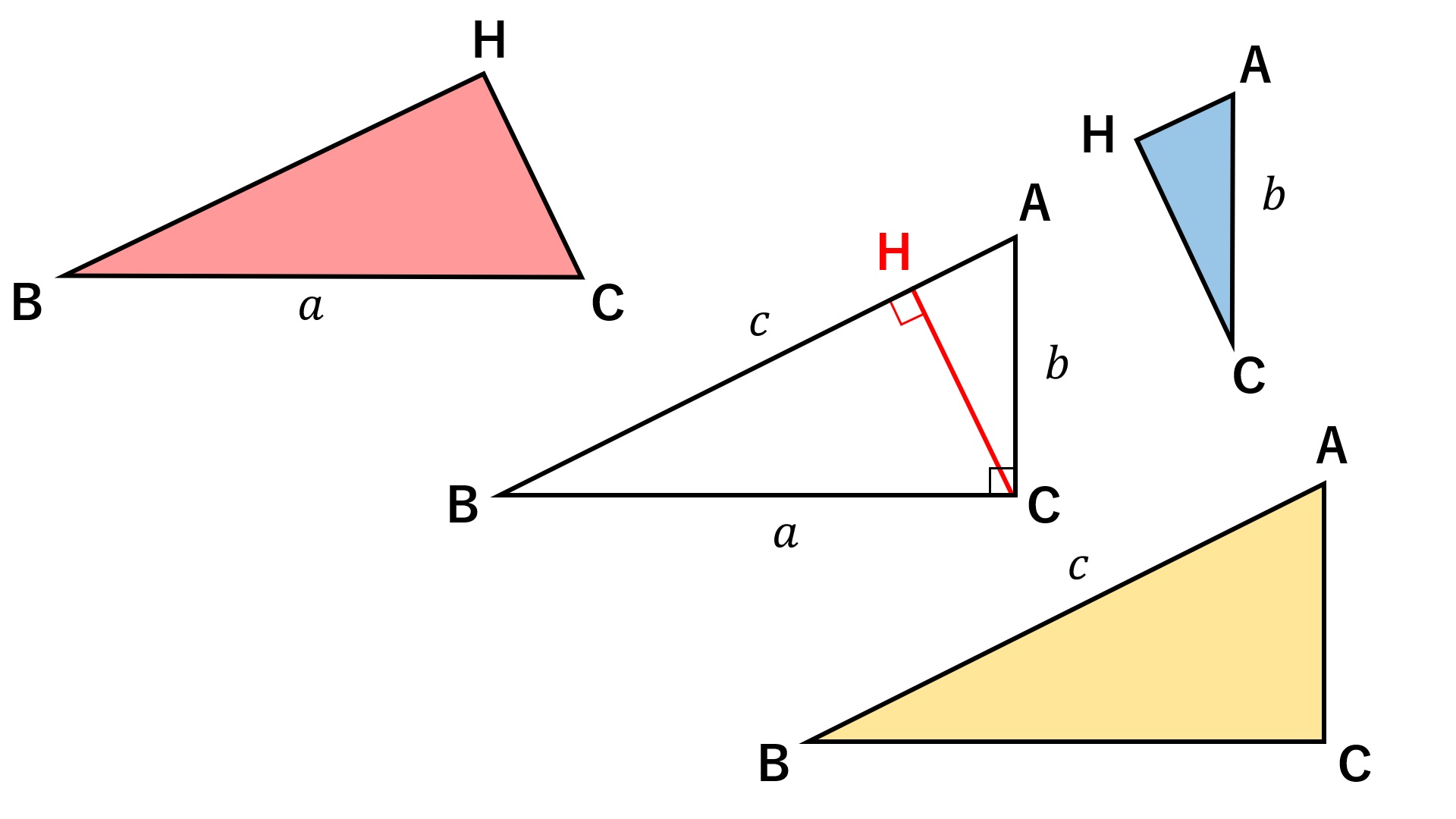
ピタゴラスの定理という名前は、ピタゴラスという名前のギリシャの数学者に由来します。 ピタゴラスは、 直角三角形の 辺の長さを見つける式を開発しました。 ピタゴラス直角三角形の各辺を正方形として扱った場合(図1を参照)、2つの最小の正方形の面積を合計すると、大きな正方形の三平方の定理による辺の長さの計算です。三平方の定理は、 直角三角形の三辺をa,b,cとする。斜辺(最も長い辺)をcとすると、 c² = a² b² が成り立つ というものです。別名ピタゴラスの定理とも呼ばれます。 式は綺麗ですが、二乗が出てきます。
Incoming Term: ピタゴラスの定理 計算方法,
コメント
コメントを投稿